Here is an explanation of a Hidato solving technique that some people might find obvious and they use it without even thinking of it as a special technique. But, for those who still struggle with the more difficult puzzles, here is a quick guide of the technique that I call “
cornering“.
It can be used when a cell has only one “
neighbor†that is an empty cell. In such a case, that cell (with only one empty neighbor), must contain a number that is consecutive to (at least) one of the already filled in neighbors.
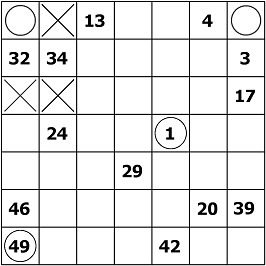
Look at the upper left corner. Number 33 could in theory go into any of the 4 cells that are neighbors to both 32 and 34. However,
it must actually go into R1C1 (row 1, column 1).
Why? Because R1C1 has only one empty neighbor and according to the rule I stated above, in such a case that cell must be consecutive to (at least) one of the existing neighbors.
Why? Because each cell (other than 1 and the largest number) must have both a “+1†and a “-1†neighbor. So, the only options for R1C1 are 31 or 33 or 35. If you put any number other than one of those in R1C1, it would have only one of the “+1â€, “-1†neighbors, because there is only room for one number next to it. That is why I also call this technique “
dead-endâ€. But 31 would be too far from 29; and 35 would be too far from 39.
Therefore R1C1=33!
Now, look at R1C7 (it’s circled). See if you can figure out why the number in that cell MUST BE 5.
 Look at the upper left corner. Number 33 could in theory go into any of the 4 cells that are neighbors to both 32 and 34. However, it must actually go into R1C1 (row 1, column 1). Why? Because R1C1 has only one empty neighbor and according to the rule I stated above, in such a case that cell must be consecutive to (at least) one of the existing neighbors.
Why? Because each cell (other than 1 and the largest number) must have both a “+1†and a “-1†neighbor. So, the only options for R1C1 are 31 or 33 or 35. If you put any number other than one of those in R1C1, it would have only one of the “+1â€, “-1†neighbors, because there is only room for one number next to it. That is why I also call this technique “dead-endâ€. But 31 would be too far from 29; and 35 would be too far from 39. Therefore R1C1=33!
Now, look at R1C7 (it’s circled). See if you can figure out why the number in that cell MUST BE 5.
Look at the upper left corner. Number 33 could in theory go into any of the 4 cells that are neighbors to both 32 and 34. However, it must actually go into R1C1 (row 1, column 1). Why? Because R1C1 has only one empty neighbor and according to the rule I stated above, in such a case that cell must be consecutive to (at least) one of the existing neighbors.
Why? Because each cell (other than 1 and the largest number) must have both a “+1†and a “-1†neighbor. So, the only options for R1C1 are 31 or 33 or 35. If you put any number other than one of those in R1C1, it would have only one of the “+1â€, “-1†neighbors, because there is only room for one number next to it. That is why I also call this technique “dead-endâ€. But 31 would be too far from 29; and 35 would be too far from 39. Therefore R1C1=33!
Now, look at R1C7 (it’s circled). See if you can figure out why the number in that cell MUST BE 5.



2 Comments
Just a thought, could you make a “Greater Than/Less Than” Hidoku and use very few given numbers?
Yes Amy! 🙂 It is possible and I’ve been thinking about the same thing but just can’t find time right now to do it… will be done next year, though.