It’s about time I finally explained the basic (and most common) Sudoku solving techniques. Most of you are already familiar with these, but for those who aren’t – I’d like to show my explanation.
These techniques are used in ALL sudoku puzzles –
Classic, Killer, Samurai and others. Make sure you fully understand them before you attempt to solve the more difficult puzzles.
I will be using one classic Sudoku puzzle in which I will demonstrate how each of the techniques contributes to the final solution.
Perhaps you’ve already seen this particular puzzle:
 BASIC TECHNIQUES
BASIC TECHNIQUES
1.
NAKED SINGLES
(aka “elimination”)
I’m sure you know this method, but lets clearly explain it anyway.
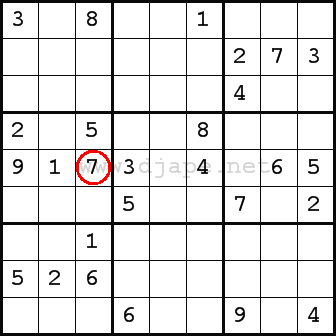
Have a look at row 5, column 3 (from now on, this will be marked as simply R5C3).
Numbers 1, 2, 5 and 9 are in the same
nonet so they can’t go into that cell.
Numbers 3, 4 and 6 are in the same
row so they can’t go into that cell either.
Finally, number 8 is in the same
column, so the only remaining number is 7. Therefore, R5C3=7 and this is a naked single. (it’s “naked” because it’s the only number that can go into one cell)
2.
HIDDEN SINGLES
(aka “singles”)
Having applied “naked singles” a few times, we come to this position:
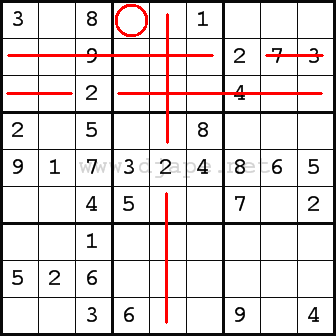
Now, focus on number 2 in the top part of the puzzle. Red lines indicate where number 2
can’t go:
– R2C7 = 2, so number 2 can’t go anywhere in R2;
– R3C3 = 2, so number 2 can’t go anywhere in R3;
– R5C5 = 2, so number 2 can’t go anywhere in C5.
When you look at nonet 2, there is only one cell that is not covered with red lines – it’s R1C4, so this is the only place in nonet 2 where number 2 can go into. Therefore, R1C4 = 2 – it’s a “hidden single”, because potentially there are other candidates for this cell (4, 7 and 9) and number 2 is hidden amongst them.
If we keep applying “naked” and “hidden” singles, we come to this stage:
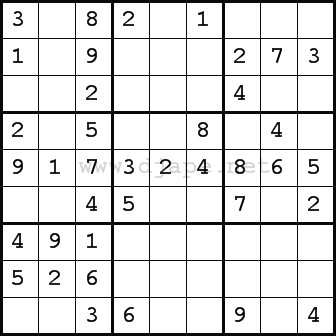
Now what?
ADVANCED TECHNIQUES
Alright, now we must start using
pencilmarks. For each unsolved cell, pencil in all the numbers that are still possible candidates for that cell (i.e. they are not in the same column, row nor nonet as that cell).
Your grid should look like this:
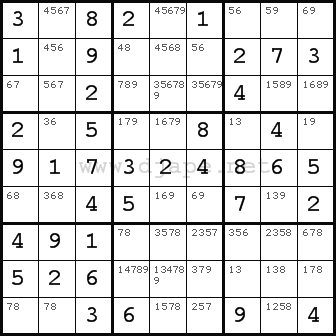
For each of the remaining 3 techniques, I will be coming back to this image.
3.
BOX BREAKS
(aka “row/column and nonet interactions”)
We again focus on nonet (“box”) 2 and row 2. Check the possible cells for number 8. In row 2, number 8 can appear only in R2C4 and R2C5. Both these cells are in nonet 2. Whichever one of them ends up being 8, number 8 will be eliminated from the rest of nonet 2. Therefore, we can do that straightaway:
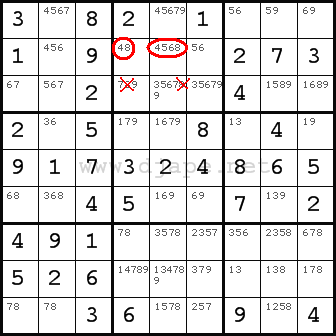
In other words, you make an intersect of row 2 and nonet 2 on one particular value and remove that value from the remainder of that nonet.
It can also work the other way – just exchange words row and nonet and you’ll get it.
So, like all remaining techniques, this technique doesn’t actually solve a cell – it only removes some candidates which then helps you in the solving process.
4.
NAKED PAIRS
Have a look at nonet 7 and row 9. In nonet 7, we know that numbers 7 and 8 must go into R9C1 and R9C2. These numbers are “naked” – there are no other candidates for those two cells except two of them. So, two numbers in two cells and no other candidates for those two cells – that’s a naked pair. When you find such two cells and they belong to the same row or column or nonet – you can eliminate those two numbers from other cells in that area.
In this case – there is nothing to remove from nonet 7 because all other cells are already solved.
But, since those two cells also both belong to row 9, there are candidates that can be removed from that row. Therefore, we remove numbers 7 and 8 from the candidates list in row 9.
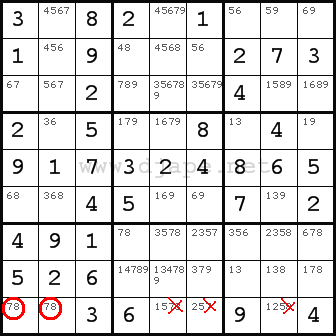
4.
NAKED SUBSETS
(aka “subsets”)
This is essentially the same technique as the previous one, except that you take more than two cells at a time.
So, what you are looking for are
“n” numbers that are candidates in
precisely “n” cells that fall onto the same nonet or column or row.
We have this case in nonet 3/row 1.
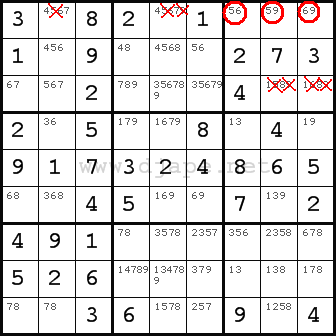 NB:
NB: What’s important to notice is that each of the marked cells has only two pencilmark values, but there are altogether 3 different numbers there. It could happen that, for example, one cell has 3 values and two cells have 2 values, but it is important that there are N different numbers in N different cells altogether.
4.
HIDDEN SUBSETS
(aka “subsets”)
So far we were only looking at “naked” subsets – subsets with no other pencilmarks in those cells.
Look at the same row again. Numbers 1 and 8 are penciled-in in only two cells – R3C8 and R3C9. Two numbers, two cells – it’s a hidden pair! When you are sure of that, you convert that hidden pair into a naked pair.
So, first you do this:
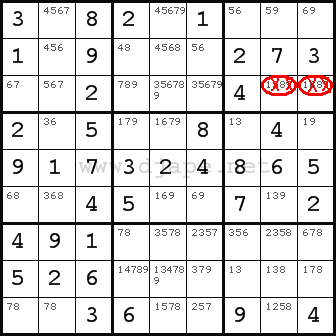
Now, the pair 1-8 has become naked in row 3 and you can remove those two numbers from the remaining cells in row 3.
…
After you have applied all these techniques on this puzzle as many times as possible, you should reach this position:
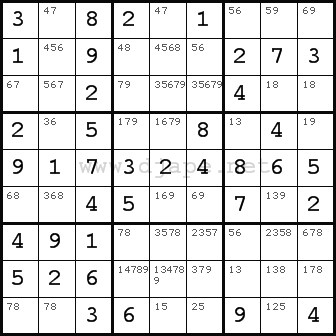
Well, to proceed further, you must learn another technique – “X-Wing”.
I’ve already explained that in detail before.
X-Wing will solve this puzzle. The final and most advanced technique is
Swordfish which is similar to X-Wing except that it applies to more than two rows/columns.
I consider all other techniques (“xy-wing”, “colouring”, “nishio”, etc.) to be a limited form of trial and error and I don’t use them for my puzzles.

 2.
2.  Now, focus on number 2 in the top part of the puzzle. Red lines indicate where number 2 can’t go:
– R2C7 = 2, so number 2 can’t go anywhere in R2;
– R3C3 = 2, so number 2 can’t go anywhere in R3;
– R5C5 = 2, so number 2 can’t go anywhere in C5.
When you look at nonet 2, there is only one cell that is not covered with red lines – it’s R1C4, so this is the only place in nonet 2 where number 2 can go into. Therefore, R1C4 = 2 – it’s a “hidden single”, because potentially there are other candidates for this cell (4, 7 and 9) and number 2 is hidden amongst them.
If we keep applying “naked” and “hidden” singles, we come to this stage:
Now, focus on number 2 in the top part of the puzzle. Red lines indicate where number 2 can’t go:
– R2C7 = 2, so number 2 can’t go anywhere in R2;
– R3C3 = 2, so number 2 can’t go anywhere in R3;
– R5C5 = 2, so number 2 can’t go anywhere in C5.
When you look at nonet 2, there is only one cell that is not covered with red lines – it’s R1C4, so this is the only place in nonet 2 where number 2 can go into. Therefore, R1C4 = 2 – it’s a “hidden single”, because potentially there are other candidates for this cell (4, 7 and 9) and number 2 is hidden amongst them.
If we keep applying “naked” and “hidden” singles, we come to this stage:
 Now what?
Now what?
 For each of the remaining 3 techniques, I will be coming back to this image.
3.
For each of the remaining 3 techniques, I will be coming back to this image.
3.  In other words, you make an intersect of row 2 and nonet 2 on one particular value and remove that value from the remainder of that nonet.
It can also work the other way – just exchange words row and nonet and you’ll get it.
So, like all remaining techniques, this technique doesn’t actually solve a cell – it only removes some candidates which then helps you in the solving process.
4.
In other words, you make an intersect of row 2 and nonet 2 on one particular value and remove that value from the remainder of that nonet.
It can also work the other way – just exchange words row and nonet and you’ll get it.
So, like all remaining techniques, this technique doesn’t actually solve a cell – it only removes some candidates which then helps you in the solving process.
4.  4.
4.  NB: What’s important to notice is that each of the marked cells has only two pencilmark values, but there are altogether 3 different numbers there. It could happen that, for example, one cell has 3 values and two cells have 2 values, but it is important that there are N different numbers in N different cells altogether.
4.
NB: What’s important to notice is that each of the marked cells has only two pencilmark values, but there are altogether 3 different numbers there. It could happen that, for example, one cell has 3 values and two cells have 2 values, but it is important that there are N different numbers in N different cells altogether.
4.  Now, the pair 1-8 has become naked in row 3 and you can remove those two numbers from the remaining cells in row 3.
…
After you have applied all these techniques on this puzzle as many times as possible, you should reach this position:
Now, the pair 1-8 has become naked in row 3 and you can remove those two numbers from the remaining cells in row 3.
…
After you have applied all these techniques on this puzzle as many times as possible, you should reach this position:
 Well, to proceed further, you must learn another technique – “X-Wing”. I’ve already explained that in detail before.
X-Wing will solve this puzzle. The final and most advanced technique is Swordfish which is similar to X-Wing except that it applies to more than two rows/columns.
I consider all other techniques (“xy-wing”, “colouring”, “nishio”, etc.) to be a limited form of trial and error and I don’t use them for my puzzles.
Well, to proceed further, you must learn another technique – “X-Wing”. I’ve already explained that in detail before.
X-Wing will solve this puzzle. The final and most advanced technique is Swordfish which is similar to X-Wing except that it applies to more than two rows/columns.
I consider all other techniques (“xy-wing”, “colouring”, “nishio”, etc.) to be a limited form of trial and error and I don’t use them for my puzzles.
7 Comments
image paths are broken
thanks salva, i fixed them now!
For the Naked Subsets, and Hidden subsets i don’t understand how knowing those facts allow us to eliminate what you did. For the Naked pairs i understand that example, but what if the nonet wasn’t filled the rest of the way or if their in the same column? I’m just not understanding the logic here :/
thank you…i think this’ll help me..if i can understand it more…thanks fer yer help…
level 2 seems hard for some reason
I do not understand the rules of SS. Looking at the Washington Post 11/6/2016 puzzle: lower right puzzle the first nonet on second row, seems to me to have no 9. The first column & third column are eliminated by the upper right puzzle. The second column is eliminated by the first nonet in third row. What rule do I not understand?
Hi Mike,
the rules of 5 interconnected sudokus do not extend outside of each 9×9 puzzle. So, the numbers in the upper right puzzle do not eliminate any numbers in the lower right puzzle. Numbers in one 9×9 puzzle affect only the numbers in the overlapping nonet of the adjacent puzzle.
I hope this makes sense and that you will now be able to solve Samurais! 🙂
Let me know if you still need my assistance.
Cheers,
Djape
3 Trackbacks
[…] Usual classic Sudoku techniques are required to solve these puzzles: naked and hidden singles, naked and hidden subsets (pairs, triplets etc) and “row/column and box interactionsâ€. For the hardest of puzzles X-Wing and Swordfish techniques might be needed. […]
[…] A while ago I explained the X-Wing solving technique. Recently I shown my explanation of other basic, Classic Sudoku solving techniques. […]
[…] Classic Techniques […]