A while ago I posted an explanation of an advanced Griddlers/Picross/Nonograms/Hanjie solving technique called
Bordering.
Here is another example of the bordering technique applied in a different way.
Consider this partial nonogram in which only the top few rows are shown. Focus on the first three rows and the “7” clues in them. Where can or cannot this “7” clue in the first row begin? Notice the circled “1” which belongs to column 5.
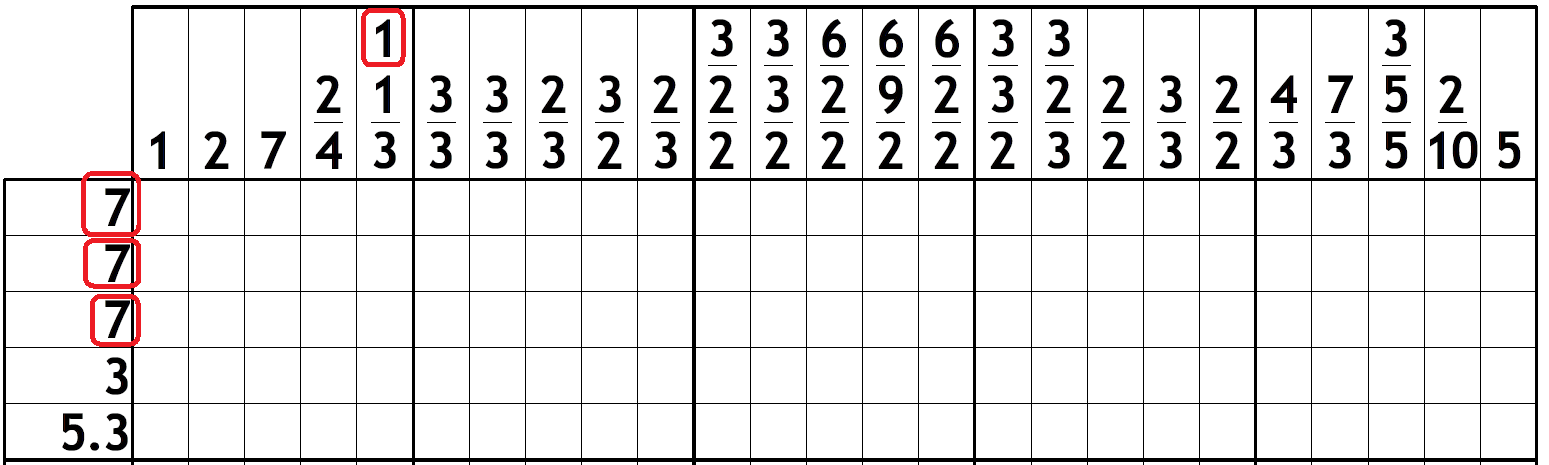
Can the “7” of the first row begin in column 1? It can’t. Why? Because if it did, the “2” in column 2 would also kick off the “7” in row 2, but the “1” in column 5 would stop it before all 7 squares in row 2 are filled, because after the “1” in column 5 there must be a blank square. Get it? Think about it for a while and consider what happens with the perpendicular lines when the “7” of the first row begins right at the start of the row.
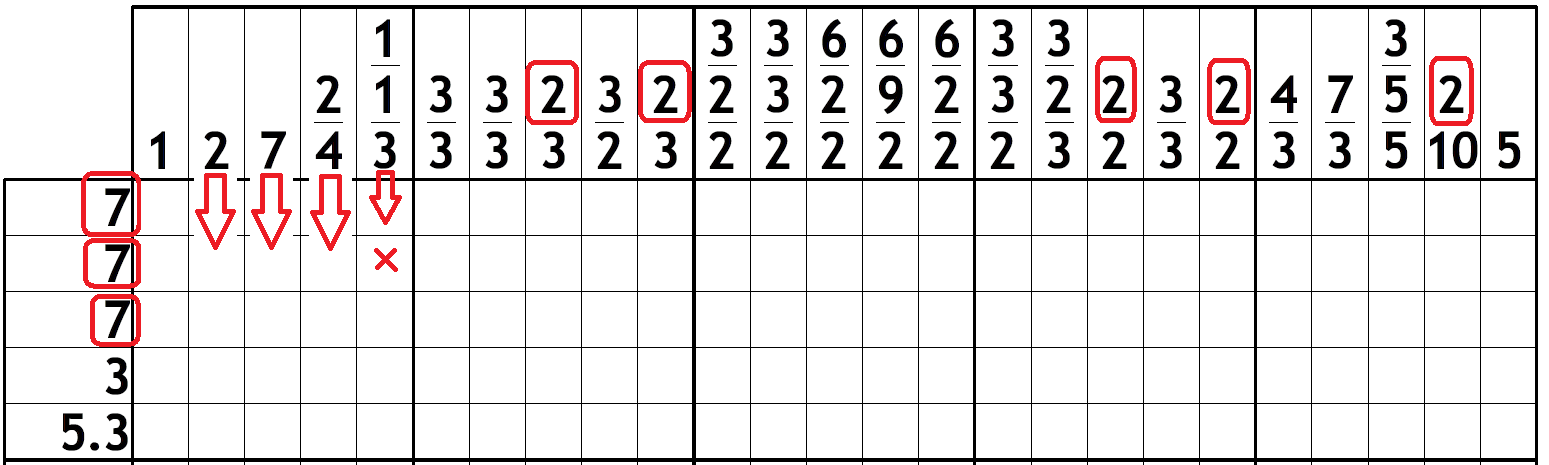
Continuing this logic, we can conclude the same for the first four squares of row 1 and get to the following position (the red “X”s mean “certain whites”).
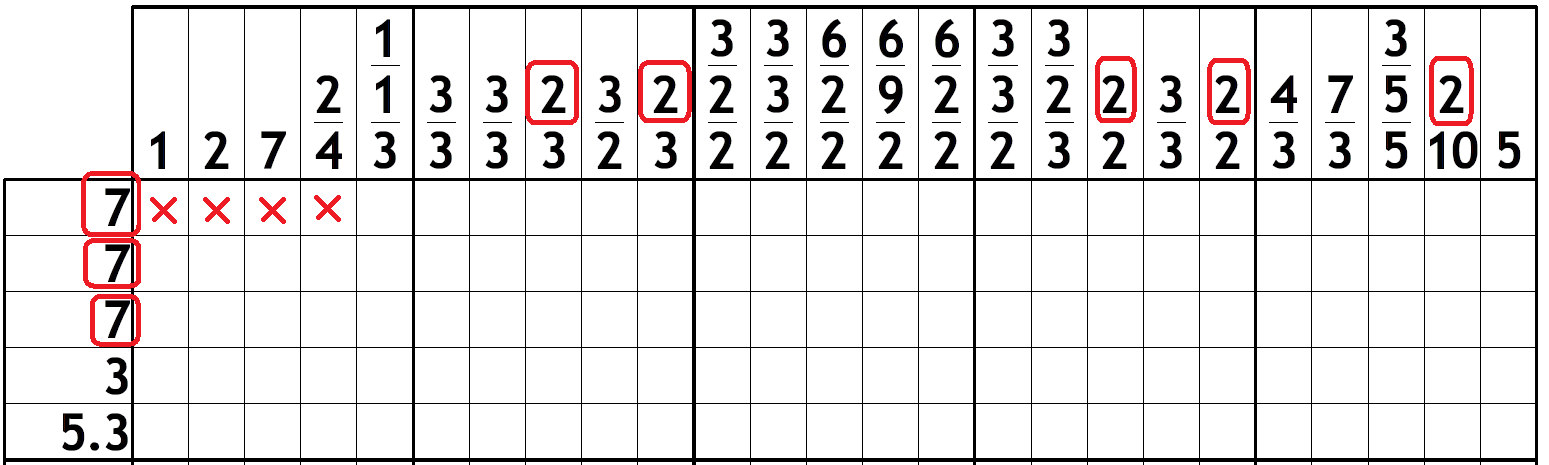
Now, let’s extend this logic to row 3. Look at all the circled “2”s, which are the first clues (this is extremely important) in their corresponding columns. Looking from the start of row 1, the first two circled “2”s prevent the “7” of row 1 starting anywhere before the “2”s, because the “3” nested between the two “2”s would extend to row 3, but it would be a lonely black square in row 3 because there would be a white to the left and to the right of it, because of the “2”s. Think about it for a while.
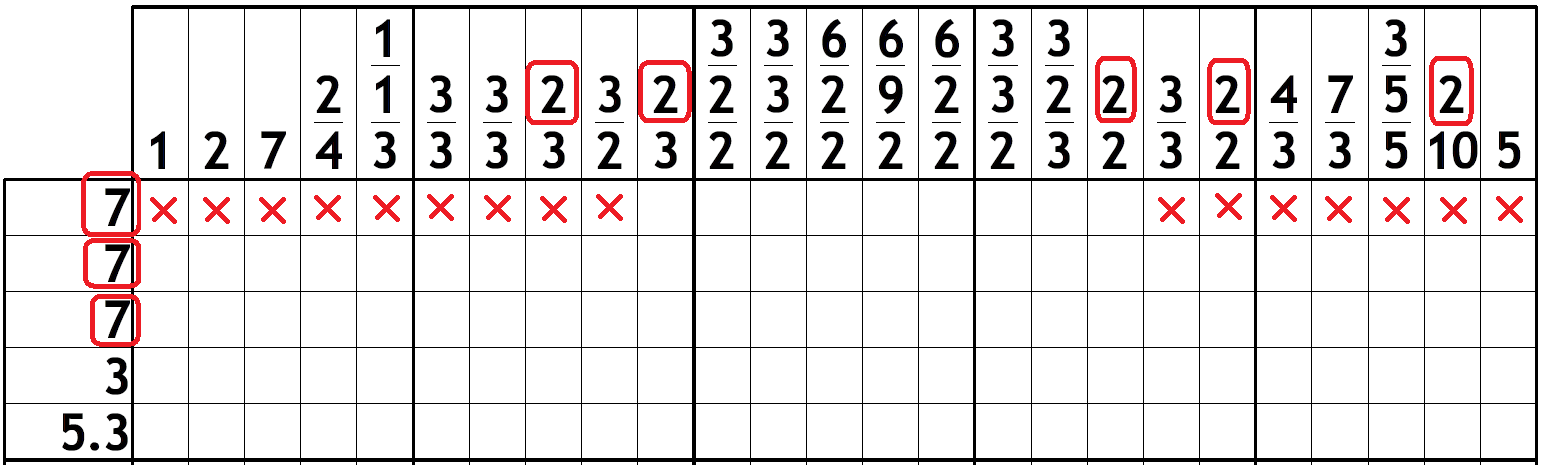
Finally, now start applying this logic looking from the end of row 1 backwards (right-to-left). The “2”s are circled and should help you conclude that none of the last 7 squares in row 1 can be black and therefore, must be white.
Does this make sense to you? Please do comment and/or ask questions if you have any doubts.
