It helps if you find a 3×3 “box” filled entirely by a few “cages” except that one (and only one) of those cages has a single cell outside of that same box. If you’re lucky enough and find such a box, you add up the cage totals for the cages from that box and subtract 45. The result is the value of that single cell that’s outside the box. This is called an “outie”.
Similarly, all but one cell of a box can belong to a few cages with no cells sticking outside the box. That one cell which belongs to another cage is called an “innie”. It’s value must be 45-(the sum of cages within that box).
Both examples are shown in this puzzle. The outie is the number 3 in a green square, and the innie is the number 8 in another green square:
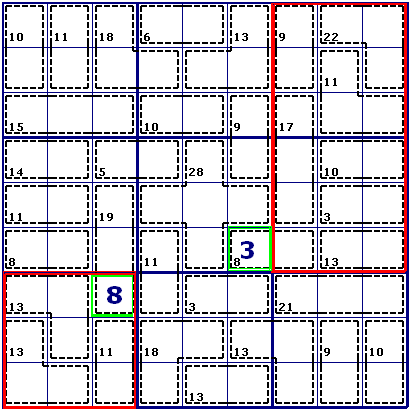 Find something strange there?
Well, the innie is just as I described: 45-(13+13+11) = 45-37 = 8.
However, the outie comes from two combined boxes. Therefore, it’s value is (9+22+11+17+10+3+13+8)-2*45 = 93-90 = 3.
You can combine any number of boxes in this way. A more difficult way to find innies and outies is by looking at rows and columns, but that will be explained some other time.
Find something strange there?
Well, the innie is just as I described: 45-(13+13+11) = 45-37 = 8.
However, the outie comes from two combined boxes. Therefore, it’s value is (9+22+11+17+10+3+13+8)-2*45 = 93-90 = 3.
You can combine any number of boxes in this way. A more difficult way to find innies and outies is by looking at rows and columns, but that will be explained some other time.
One Comment
Awesome! This is exactly some of the help I was looking for.
2 Trackbacks
[…] The basic idea is similar to “innies” and “outies” except that you’re not looking for one cell but for any number of them. See the explanation of innies/outies here. […]
[…] Killer Sudoku, but it’s a 10×10 Zero Killer in which you use all 10 digits, from 0 to 9! The rule of 45 applies, but be careful when you analyze the sums! For example, 3 over two cells can now also be […]