Diagonal and nonet interaction
This one is a simple extension of the “row/column and nonet interaction technique”. Just look at this sample puzzle which has been solved using the standard techniques up to this point: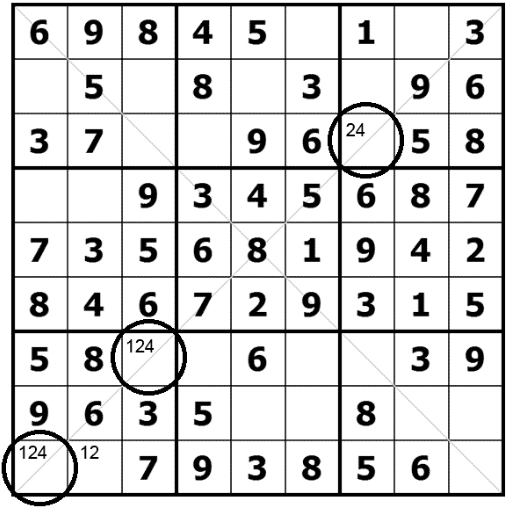
Focus on the number “4” in the bottom left nonet. Out of three unsolved cells, the number 4 can go into only two of them: R7C3 and R9C1. As it happens, both of those two cells are on the diagonal. Can you see what I mean? Well, when that happens, it means that the number 4 cannot go anywhere else on the diagonal, outside of this nonet. Get it? Again: 4 is a candidate in one nonet ONLY in cells which belong to a diagonal. Whichever one the 4 goes into, it will be on a diagonal and therefore, we can eliminate the 4 from the rest of this diagonal, outside of the nonet. So… now we look at the rest of this diagonal and find that in the top right nonet, number 4 can be eliminated from one unsolved cell (R3C7) of the diagonal, which in turns effectively solved this cell – since it can’t be 4 it must be 2 (the only remaining candidate for that cell). Get it?
Diagonal Sudoku Crossover technique
This technique is somewhat similar to the previous one. Let’s look at another sample puzzle.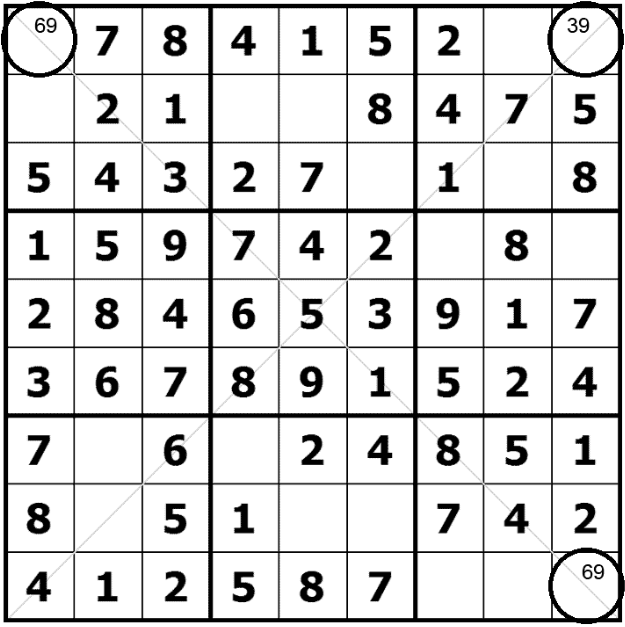
First, focus on the main diagonal. Number 9 has to be somewhere on this diagonal and as you can see, the only two options are R1C1 (upper left corner) and R9C9 (bottom right corner). In such case, when there are only two cells on a diagonal that could potentially hold a number, we can apply the Crossover technique. How?Well, let’s assume that number 9 goes into R1C1. In that case, 9 would be eliminated from the rest of R1 and C1. If 9 went into R9C9, it would be eliminated from R9 and C9. Either way, wherever 9 goes, it would be eliminated in the intersection of those rows and columns, in other words, where the imaginary lines, two horizontal and two vertical, cross. So, 9 can be eliminated from R1C9 (and also from R9C1 but that cell is already solved), which solves that cell: R1C9 = 3 (the only other option). Hope this was helpful and clear enough. 🙂
