The Law of Leftovers (LOL)

I promised to explain this technique, which applies to Jigsaw Sudoku (aka irregular blocks) puzzles, a while ago, so it’s time to keep the promise. You can find the same technique explained on various other sites, too. This technique is somewhat similar to innies/outies which is used for solving Killer Sudoku puzzles, but there is no math involved and, again, it applies to Jigsaw Sudokus (and variations thereof). First, I’ll explain some terminology that will be used: LOL can be applied to any number of either rows or columns. How many rows you will use, it’s up to you (depending on the puzzle you are solving). The rows you are using must be adjacent to each other and they can start from the middle. In other words, they can, but don’t have to, be aligned to the edge of the puzzle. The adjacent rows (columns) that you choose to apply LOL, we will call AREA. Some jigsaw nonets will be completely outside your chosen area, some will be completely inside it and some will have cells both inside and outside your area. Focus on nonets that have cells both inside and outside the area. We’ll call them BROKEN NONETS. INNIES are cells that are within the area and belong to broken nonets which have fewer cells inside the area than outside of it. OUTIES are cells that are outside the area and belong to broken nonets which have fewers cells outside the area than inside it. 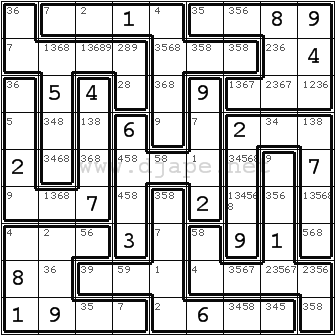Ok, this sounds quite confusing. So here is a sample puzzle to make it clear: By using the common Sudoku solving techniques, you should reach this position: Now what? Look at the first 3 columns. This will be your area. It is outlined in red in this picture: If you are paying attention, you will already know why are some cells outlined in green. They are innies and outies. If you are not sure why, read the definition of innies and outies again! IMPORTANT: The number of innies must always be equal to the number of outies. If your number of innies doesn’t match to your outies, you’ve done something wrong. Go back and look at it again! Finally, it is time to state

The Law of Leftovers

The set of numbers in innies must be the same as the set of numbers in outies.

Why? Because in your area, which consists of “N” rows, there must be precisely “N” occurences of each digit (1-9 in normal Sudoku case). This is always the case in any Sudoku puzzle. Also, any “N” nonets contain precisely “N” times each digit (1-9). Now, jigsaw nonets that are broken by this area, “borrow” (or “lend”, depends how you look at it) some of their numbers from the rest of the puzzle. Those are innies and outies. In order to keep the puzzle consistent, those numbers that are borrowed must be the same as the numbers that are lent. Anyway, lets apply LOL to our sample puzzle. Our 3 innies have these candidate numbers (some of them are naked singles, but it doesn’t matter): 7, 2 and 3|9. Our 3 outies can be: 2|8|9, 2|8 and 7. So, number 3 is a candidate in innies, but it’s not a candidate in outies. According to the Law of Leftovers, this cannot be! Therefore, we can eliminate 3 from the list of candidates in innies. Accordingly, we can eliminate 8 from outies (because it does not appear in the list of candidates for innies). There you go! We have solved two cells: R3C4=2 and R8C3=9. From here, this puzzle can be solved by using the usual techniques. Here is the final solution. Obviously, LOL can be applied to Jigsaw overlapping Sudoku variant puzzles (Samurai, TwoDoku and any other) as well, using the same approach.