Another overlapping sudoku variant – now with 3 Sudoku X puzzles.
Warning: This puzzle is quite difficult even that it can be solved using only basic sudoku solving techniques. You must work on all three puzzles in order to get the solution. Also, I think you might get confused about the “fourth” puzzle which you might think exists in the center of the entire puzzle. Well – it doesn’t! The middle 9×9 does not have to be a valid puzzle! Look at the diagonals – they well define which 3 puzzles must be solved.
You can use the Twin Nonets technique, too!
(click to download or right-click to save the image!)
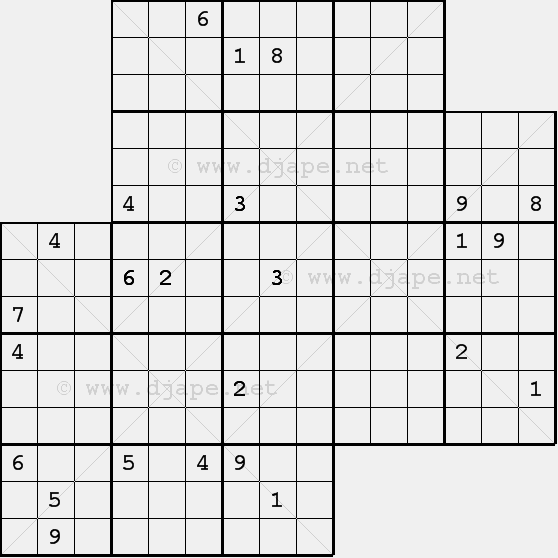 |
|
| |
To see the solution to this puzzle click here



14 Comments
Just wondering why people seem to find Xs harder than regular sudoku, as gleaned from their comments and djape’s remarks when he posts them. Surely the more constraints placed on the numbers, the easier the puzzle? — At least that’s what I’ve found. Not that this weekend’s quintuple puzzle was easy, despite the extra help!
Diana
Hi Diana,
Your observation is not entirely correct. The more constraints – the more “techniques” you must apply to solve the puzzle. Or, you could say it another way – the more constraints – the fewer starting clues need to be in the puzzle.
Consider Killer Sudoku. They have so much more constraints than classic Sudoku yet they are so difficult. This is because there are fewer clues in the starting grid.
I couldn’t get into this one at all – pls help!! I realise that the first and fourth nonets (in the same row or column) in certain cases will be the same, and I know that it is an ‘X’, but I still cannot get anywhere… 🙁
I am with you mate. I have only three definites, 2 4’s and an 8 and am now stuck.
Help
Dom, you should look for hidden singles on the diagonals in the “bottom” puzzle… you can find a few clues there (another 4 and a 9 to be more specific)… Focus on the number 4 in the bottom puzzle – you should find a few of those.
Then there is a hidden single for number 2 on one of the diagonals in the “top” puzzle…
I’m not going to reveal too much 🙂
what’s a ‘hidden single’?
A naked single is when you eliminate 8 values from one cell, so the remaining value must be it.
A hidden single is when you eliminate one value from 8 cells in a row/column/nonet/diagonal, so that value must go into the remainining 9th cell. In other words, there is only one spot in which the number can go, so it must be there.
Those two are the two basic solving techniques.
Can you explain why there is a single 2 in the top box? I can see an altenative on the diagonal in the same box?
Emma, download this file: http://www.djapedjape.com/download/images/solution_triple20051128_2-s.png
It shows a few clues that you should be able to find just by using simple elimination. You can then eliminate a few more candidates in the “bottom” puzzle which affect the rest of the full puzzle.
OK. I am officially frustrated by this one. I got all the 4s in the lower sudoku plus a 9, 8 and a 4. I took a gander at the hint you posted to Emma, and I can’t verify how you determined without a doubt how to get the 8 in the nonet with the 6 and 2 provided as starters. I have not been successful at eliminating the 1 and 9 as possibilities in the cell. That 8 is holding me back from the other eliminations that are necessary to complete the puzzle. Can you help?
Rapper, in order to solve that 8 you must apply the “new solving technique” that I have been referring too. That technique is a consequence of the “naked/hidden subsets” technique, but it can be applied directly.
Basically, in the overlapping puzzle where you look at a row of 12 cells that belong to two constituent sub-puzzles, the six cells in the middle belong to both puzzles, so the 3 cells on the left and the 3 cells on the right must contain 3 same numbers, altho not neccesarily in the same order.
In the nonet in question, in the row above 6 and 2 on the far right hand side there are numbers 1 and 9 so they must appear in the same row in this nonet. This is how you eliminate 1 and 9 from other cells in the nonet.
I will write a post with an image explaining this “new technique” later.
I see it. Grrrrrrrrrrrrrrr.
The famous Aeschylus who once said the quip – I would far rather be ignorant than wise in the foreboding of evil.
This was a fabulous puzzle, ground it out on two weekend cross country flights. As noted above working all three sets of diagonals was the key for me.
DJ – let’s get more of these!
N8
One Trackback
[…] Triple X Sudoku / Gattai Half-Near-3 sudoku puzzles at any N2 odd-n size […]