Here is another novelty: Binary Puzzles, also known as
TAKUZU.
Binary Puzzles are played on square grids of any even size: 6×6, 8×8, 10×10 etc.
Your goal is to fill the grids with 0s and 1s, following these simple rules:
1. There can be at most two 0s or at most two 1s next to each other, horizontally or vertically. So, 00 and 11 are ok, but 000 and 111 are not ok; also, 010 and 101 are totally fine.
2. There must be an equal number of 1s and 0s in each row and in each column.
3. Two columns cannot be completely the same. Neither can two rows be the same.
And that’s all!
Binary Takuzu Puzzle: 12×12 WARNING: DIFFICULT!
Click on the puzzle thumbnail to access the puzzle.
How to solve Binary Puzzles
Well, the basics are very simple and follow directly from the rules just explained. Let’s see these examples:
From 1st rule we conclude that the first and second “?” must be 1. Also, from the same rule, the third “?” must be a 0. That’s easy.
There are already five 1s in this row of 10 cells. Therefore, in order to abide by the 2nd rule, the remaining two spots must be filled with 0s!
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | | | | | | | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | x | xx | 0 | 1 |
This is only a part of a puzzle. See how first row is completed and the 3rd row is almost the same as the first one. If x=0, then because of the 2nd rule xx=1, but then the 1st and the 3rd rows would be completely the same! Therefore, x=1 and xx=0!
Finally, let’s look at a slightly more complex position:
Here, there are already four 0s filled in. There can be only one more 0 in this row! Can the “?” be “0”? No! Why? Because the three blank cells would all have to be 1 and since they are all adjacent, this would be against the 1st rule. Therefore, there must be a “1” in place of the “?”.
Got it? Every time there is only one occurrence of a digit missing in a row, check where it can or cannot go!
What do you think?
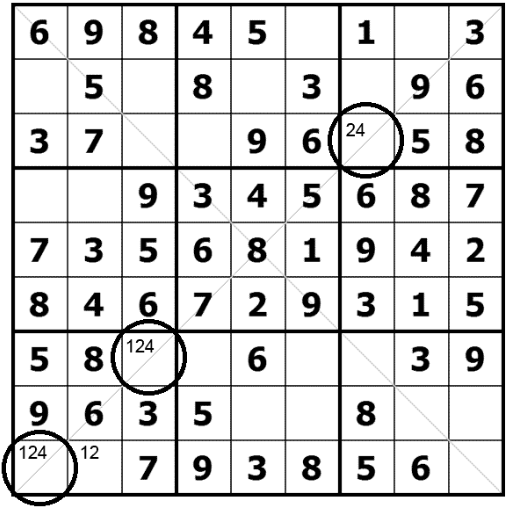Focus on the number “4” in the bottom left nonet. Out of three unsolved cells, the number 4 can go into only two of them: R7C3 and R9C1. As it happens, both of those two cells are on the diagonal. Can you see what I mean? Well, when that happens, it means that the number 4 cannot go anywhere else on the diagonal, outside of this nonet. Get it? Again: 4 is a candidate in one nonet ONLY in cells which belong to a diagonal. Whichever one the 4 goes into, it will be on a diagonal and therefore, we can eliminate the 4 from the rest of this diagonal, outside of the nonet. So… now we look at the rest of this diagonal and find that in the top right nonet, number 4 can be eliminated from one unsolved cell (R3C7) of the diagonal, which in turns effectively solved this cell – since it can’t be 4 it must be 2 (the only remaining candidate for that cell). Get it?
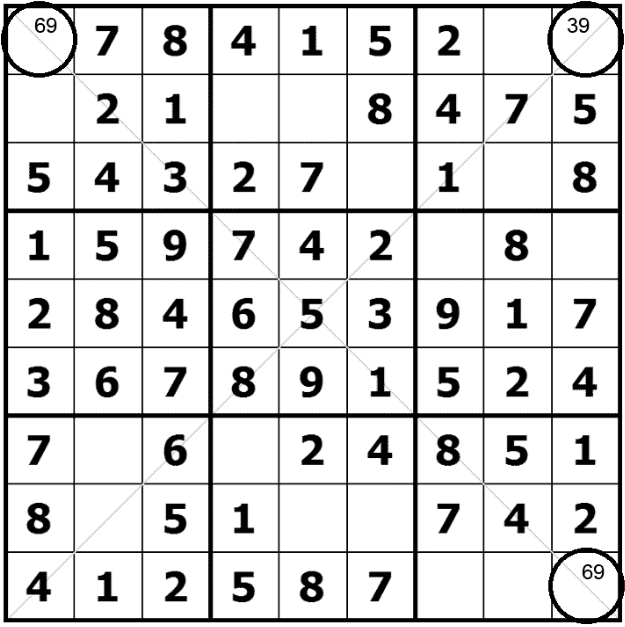First, focus on the main diagonal. Number 9 has to be somewhere on this diagonal and as you can see, the only two options are R1C1 (upper left corner) and R9C9 (bottom right corner). In such case, when there are only two cells on a diagonal that could potentially hold a number, we can apply the Crossover technique. How?